景程通信故障(雪佛兰景程ABS故障)
雪佛兰景程U0073.收到控制模块通讯总线A关闭无?
控制模块通信总线断开,设置故障码的条件是控制模块尝试在串行数据电路上建立通信在5s内超过3次,无效。 可能的故障原因有:
①TCM(网关接收变速器)电源或搭铁在行驶中突然中断,导致TCM控制模块整体停止工作;
②TCM控制模块的CAN通信启用线在行驶中突然断开或者电压过低,会引起TCM控制模块CAN BUS通信中断;
③TCM控制模块内部故障。

通信基本问题
通信最基本问题是:在信道的约束下,尽可能的提高传输速率
由于 传输速率 = 带宽 * 频谱利用率
传输速率的问题可看作提高带宽,提高频谱利用率两个子问题
带宽
现在所指“通信”实际是“电信“,即电磁波为介质的通信
通信起源于18世纪电报的出现,当时的信道是电缆
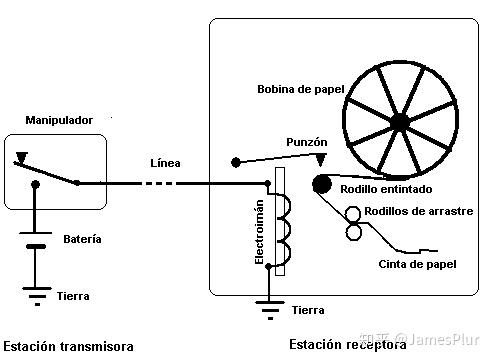
电信道
模拟一个最简单的电信道的通信系统
拿一根铜线,一个开关,一个示波器,一块电源,连成一个回路
开关开,示波器是一个高电平,记为’1‘
开关闭,示波器是一个低电平,记为‘0’
反复操作开关便可以传递信息
如果我每秒操作一次开关,传输的信息速率是1b/s
如果假设我可以无限制的加快操作速度,是不是传输的信息速率也会无限大?
显然不是
高速操作开关时,在铜线中所传递的电压信号的频谱中的高频成分的功率很高
即将信号看作是不同频率电磁波的加和,其高频电磁波的功率很高
而铜线是一个典型的低通系统,即对高频信号的阻抗很大
所以高速信号在铜线中会发生比较大的衰减,接收端会无法分辨是‘0’还是‘1’
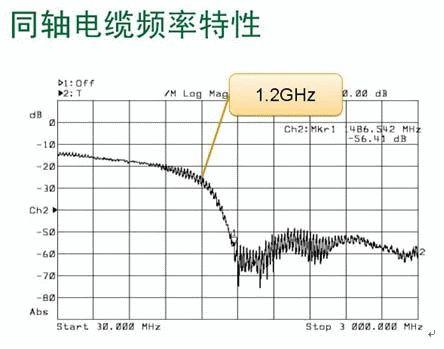
低通特性是早期传统电传输线的一个共性
包括:同轴电缆(AV线) 架空明线(老式电话线)双绞线(网线)等
传输线理论这门课程从电路的角度,详细研究了这些电传输线的性质
但是近年,现在很多学校都不开设这门课了
原因之一是电传输线已基本被光纤所取代,用电路理论来分析信道显得有些过时了
有线通信早已进入光纤的时代
光纤
光纤的最大优势就在于传输速度快
这里需要澄清的是,光纤的传输速度快和光速是没有关系的
光在光纤中的传播速度和电在铜线中的电子传导速率相仿,都接近光速
实际因为光在光纤中是全反射,走的路径长,还比铜线的传导速率慢一些
光纤的速度快,更准确来说是带宽大
那带宽是什么?
上节说铜线是一个低通系统,只允许低频信号通过
称铜线能够允许通过(衰减不超过2db)的信号频率范围为铜线的带宽(通频带)
铜线的带宽越高,显然我可以操作的开关频率便越高,传输速率也就越高。
信道的带宽,决定了信号传输速率的上限
而光纤的频率特性大概是这样:
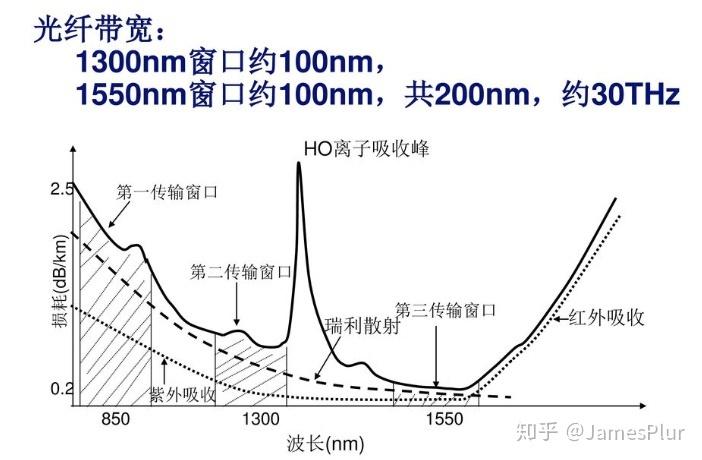
可以看到光纤的带宽在消除水锋之后有100T,一个工作窗口就有30T
同轴电缆则只有1.2G
所以光纤的传输速率上限比同轴电缆高很多,比铜线高更多(简单铜线的传输特性更差)
这也就是为什么光纤速度快
目前在实验室中,只一根光纤就已可以达到100tb/s以上的速率
实际在谈衰减的时候,距离是个非常重要的指标,以上讨论为了简便都忽略了
在短距离情况下,普通电传输线的带宽也能满足目前的需求
所以现在家里还用网线(双绞线)接光猫
频谱利用率
提高频谱的利用率的方法就是调制,调制的目的就是提高频谱利用率
高阶调制
对于开头铜线通信的那个例子
开闭开关就是一种调制,有就是‘1’,没有就是‘0’
可以换一种调制方式:以电压的大小来携带信息
比如:电压在1v以下时,为‘00’,在1v-2v时,为‘01’,在2v-3v时,为‘10’,在3v-4v时,为‘11’
这样我可以在不改变信号频率的情况下,将信息传输速率提高一倍
这就是通过调制来提高频率利用率的一个例子
但是如果我将电压的范围无限细分,是不是传输速率也可以无限提高呢?
显然不是
这是因为接收信号总是存在一定的噪声
比如接收机的热噪声
由于噪声的存在,无法将电压的幅度分的过细,否则将难以分辨电压幅度属于哪个范围
所以在通信中,信噪比是一个非常关键的存在
如果信噪比足够大,信号功率足够强,往往意味着更高的频谱利用率
频谱搬移
对于光纤和无线通信来说
信道的通频带都是”带通“的,只能传输带通信号
(实际低通信号也可以看作带通信号的一种特殊形式,即中心频率为零的情况)
带通信号的一般形式如下:
f是带通信号的中心频率
A和 代表了带通信号的幅度和相位(都是关于时间的函数,公式中为了简便没有体现出来)
可以看到,带通信号也可以表示为
其含义为,任何带通信号可以表示为一个复信号搬移到特定的频率f附近
复信号是实际不存在的,可以理解为分析信号的工具
如果简单的将实信号搬移到中心频率,会造成巨大的频谱浪费
带通信号的另一个等价形式是
这个形式显示了怎么物理实现复信号的搬移,即IQ调制
它也显示了,一个带通信号其实是由两个正交信号所张成的
所以可以把带通信号想象成一个二维平面
a和b就是x值和y值,相位 和幅度A都可以用a和b表示
各种相位调制,强度调制,QAM调制,本质上都是这个式子
上面提到了信号正交的概念,
余弦信号,正弦信号,以及它们的倍频信号都是正交的
(所谓正交,是指互相关函数恒为零,即相乘再积分为零)
只要信号是正交的,就可以通过简单的相关运算进行解调,对于接收十分有利
从这个角度考虑,为了进一步提高频谱利用率,信号可以表示为任意正交信号的加和:
这便是OFDM 正交频分复用的基本思想
总结
通信的基本问题是在信道的约束下,尽可能提高通信的传输速率
这种约束主要体现在带宽和噪声上
由此可以建立信道的基本模型:具有加性高斯白噪声的带限信道(AWGN信道)
在这个模型下,香农推导了理论上通信的极限速度:
其中C是信道容量(传输速率上限),W是带宽,S/N是信噪比
香农公式在理论上升华了通信的基本问题,为通信技术的优化提供了明确的方向
不过在实际中需要考虑的信道并不是严格的AWGN信道
比如无线通信中的时变问题,光纤在功率过大时存在不可忽略的非线性效应,无线光通信中难以处理的大气湍流效应,能对这些信道问题准确的建模,是通信技术继续优化的重要条件






